机器学习杂记

线性可分SVM:

• 主要参考这样一步一步推导支持向量机，谁还看不懂？,及【机器学习】支持向量机 SVM
• 优化公式:
  • $$D = \frac{||\omega^Tx+b||}{||\omega||}$$
  • $\omega$和$b$为超平面有关参数;
  • 定义$\omega^Tx+b\geq 0$的为正样本(y=1), 反之($\leq$)则为负样本(y=-1)
  • 则有:
    • $$\frac{y_i\times(\omega^Tx+b)}{||w||\times D}\geq 1$$
    • 仅当样本点为支持向量时, 等于$||w||\times D$,
    • 此时的D为超平面的间隔, 也是我们想要最大化的对象;
  • 故而所求变为:
    • $$D = \max\frac{(\omega^Tx_{sup}+b)\times y}{||w||}$$
  • $x_{sup}$表明它为支持向量, 总是在超平面上, 不影响最优化结果, 式子变为:
    • $$D = \max\frac{1}{||w||}$$
  • 等价于:
    • $$D = \min||w||$$
  • 为方便计算,将式子化为:
    • $$D = \min\frac{1}{2}||w||^2$$
  • 约束条件为:
    • $$(\omega^Tx+b)\times y\geq 1$$
    • $$\Rightarrow g_i(\omega,b)=1-y_i(\omega^Tx_i+b)\leq 0$$
• KKT条件:
  • $$\frac{\partial L}{\partial w_ {i}} = \frac {\partial f}{\partial w_ {i}}+\sum^{n}_{j=1} \lambda _ {j}\frac {\partial g_ {j}}{\partial w_ {i}} =0\\ \lambda_ig_ {i} (w)=0\\ g_{i} (w) \leqslant 0\\\lambda_i>0$$
• 引入松弛变量:
  • $$g_i(w)\leq 0\Rightarrow h_i(w)=g_i(w)+a_i^2=0$$
  • $$\Rightarrow L(w,\lambda,a) = f(w)+\sum_{i=1}^n\lambda_i\times[g_i(w)+a_i^2]$$
  • $$= f(w)+\sum_{i=1}^n\lambda_i\times g_i(w)+\sum_{i=1}^n\lambda_i\times a_i^2$$
• 因为
  • $$\lambda_i\geq 0\\\Rightarrow \sum\lambda\times a_i^2\geq0$$
• 故原式变为
  • $$L(w,b)= f(w)+\sum_{i=1}^n\lambda_i\times g_i(w)$$
• 当 $f(w)$ 取到最小值 $p$ 时, 我们得到最佳参数,然而由于约束的存在,
  我们不一定能够取到最小值,只能尽量接近;
• 由于
  • $$\sum_{i=1}^n\lambda_i\times g_i(w)\leq 0$$
• 所以
  • $$L(w,b) \leq p$$
• 故而我们需要先尽可能接近 $p$
  • $$\max_\lambda L(w,b,\lambda)$$
• 接着再求总体最小值
  • $$\min_{w,b}\max_\lambda L(w,b,\lambda)\\ s.t.\qquad\lambda _ {i}\geqslant 0$$
• 从而可以构造Lagrange函数:
  • $$\min_{w,b}\max_\lambda L(w,b,\lambda)=\\\ \frac{1}{2}||w||^2+\sum_{i=1}^m\lambda_i\times[1-y_i(w^Tx+b)]\\ s.t.\qquad\lambda _ {i}\geqslant 0$$
  • 注意维度问题, $\omega$ 维度与样本个数相同, 而 $\lambda$ 维度与一个样本点的特征数相同(即 $m$)
• 强对偶性转换(与KKT互为充要条件, 前面已满足),等价于
  • $$\max_\lambda\min_{w,b} L(w,b,\lambda)$$
• 由此我们可以先求 $\min_{w,b} L(w,b,\lambda)$
  • $$\frac{\partial L}{\partial w} = 0\\\frac{\partial L}{\partial b}=\sum_{i=1}^m{x_y\times y_i} = 0$$
• 第一个式子怎么求($\frac{\partial L}{\partial w} = 0$)?
  • $$L(w,b,\lambda)=\frac {1}{2}||w|^ {2}+\sum_{i=1}^{m}\lambda_i\times(1-y_ {i}(w^ {T}\vec{x_ {i}}+b))$$
  • $i$ 表示第 $i$ 特征, $m$ 为总特征数;
• 具体推导建议查看这样一步一步推导支持向量机，谁还看不懂？;

Adaboost推导

Adaboost基本流程:

• 输入: Datasets: {…,[$x_i$,$y_i$],…};
• 学习器: $F(x) = sign(F_m(x)) = sign(\Sigma_k^M{F_k(x)\times \alpha_k})$;
• 参数:
  • $W_i, i = 1…N$: 各个样本点的权值;这一权重代表了被分类错误的严重性,也即当一个学习器分类;
  • $\alpha_k$:各个学习器的权值;

流程:

• 初始化样本点权重: $W_i = 1/N$;
• 迭代:
  • 训练一个弱学习器$G_k$,G 代表 gender;
  • 更新$\alpha_k,W_i$:
    • error rate:
      • $$e_m = \Sigma_i^N{W_i\times I(G(x_i)\ != y_i)}$$
    • the weight of the Gender learner:
      • $$\alpha_k = \frac{1}{2}\log{\frac{1-e_m}{e_m}}, i.e.\frac{1}{2}\log{\frac{positive\ rate}{negative\ rate}}$$
    • The weight of each sample points:
      • $W{k,i} = W{k-1,i}\times \exp{-\alpha_m\times y_i\times G_m(x)}$
    • $Fm = F{m-1}+\alpha\times G(x)$
• 最终学习器:$F(x) = sign(F_m(x)) = sign(\Sigma_m^M \alpha_mG_m(x))$

更新公式的推导

• Loss function:
  • Loss = $\exp(-yi\times[F{m-1}(x)+\alpha_m\times G_m(x)])$
    • $= \exp(-yi\times F{m-1}(x))\times\exp(-y_i\times\alpha_m\times G_m(x))$
    • 定义:$Wi = \exp(-y_i\times F{m-1}(x))$
    • $= W_i\times\exp(-y_i\times \alpha_m \times G_m(x))$
  • 故而损失最小化也即:
    • $W_i$已知;
    • $G^*(x) = \alpham\times G_m(x) = \argmin{\alpha,G(x)}[{\exp(-y_i\times \alpha_m \times G_m(x_i))}]$
    • 由于要在整个训练集上最小化损失,故而要将其期望最小化:
      • $$E[Loss] = \exp(-\alpha \times y_i \times G_m(x_i))\\ => \exp(-\alpha)\times P(y=G_m(x))+\exp(\alpha)\times P(y != G_m(x))$$

        离散型变量的期望求和公式;

      • $$-\exp(-\alpha)\times P(y=G_m(x))+\exp(\alpha)\times P(y != G_m(x))==0$$

        求导并使其等于0, 从而找到最小点;

      • $$\alpha_k = \frac{1}{2}\log{\frac{1-P(y != G_m(x))}{P(y != G_m(x))}}$$

        $\alpha$更新公式;

损失函数:

• 类型:
  • 0-1损失:
  • 平方损失:
  • 绝对损失:
  • 对数损失:
• 直接将(f(x),y)带进Loss函数去算,得到的是单个预测的损失;
• 我们要验证决策函数f的优良性, 应当求其期望:
  • 输入输出遵循联合分布P(X,Y),则期望损失:
    • $$R_{exp}(f) = E_P[L(Y,f(X))] = \inf_{\kappa\times y}L(x,f(x))P(x,y)dxdy$$
  • 然而我们无法知道P(X,Y) [这正是我们需要的], 故而我们只能用已知的—训练集的损失, 也即经验损失:
    • $$R_{emp}(f) =\frac{1}{N}\sum_{i=1}{N}L(y_i,f(x_i)$$
  • 根据经验风险最小化求最优:
    • $$\min_f \in F{\frac{1}{N}\sum_{i=1}^N{L(y_i,f(x_i))}}$$
  • 就如同下图, 忽略黑线, 能够直接取到最中心的等值线[最小值];
    • 
  • 然而我们在这种情况下求到的只能是过拟合的, 因为根据大数定律, 只有当样本量无穷大的时候,我们才能让经验风险接近期望风险;
  • 我们当然不希望过拟合(这意味着我们得到的模型只是贴近于训练数据集),因此我们要为其加上正则项:
    • $$R_{srm}(f) =\frac{1}{N}\sum_{i=1}{N}L(y_i,f(x_i)+\lambda J(f)\\ srm = structural risk minimization\\ J(f) = 模型复杂度$$
    • 关于正则化可查看什么是正则化
    • 这时,当结构风险过小,也即模型过于复杂时[含有多个非零参数],第二项模型复杂度会比较大,因而不会被选取;
• 泛化误差: 刚才我们讲到的是对于训练数据集的风险, 最小化其得到模型f,用这个模型去预测没被用来训练的数据, 就可以得到泛化误差:
  • $$R_{exp}(\hat{f}(X)) = E_P[L(Y,\hat{f}(X)] = \inf_{\kappa\times y}L(x\hat{f}(X))P(x,y)dxdy$$
  • 泛化误差也叫out of sample error,因为是经过最小化风险得到的模型, 参数已然确立, 相当于测定模型离真实值的偏离程度;

正则化作用:

• L1正则化: $\alpha||w||_1$, 1-范数
  • 权值向量各个元素的绝对值之和
  • 作用:
    • 偏向于让权值向量在优化过程中接近于0,即变得稀疏;
  • 原理:
• L2正则化: $||\alpha||w||_2^2$, 2-范数的平方
  • 权值向量各个元素平方和的平方根
  • 作用:
    • 对于大数值的权值向量进行惩罚, 从而更偏向分散的权重向量;[也即使用更多特征,从而能够减少过拟合]

原理:

• 我们求解实质上是优化问题, 最小化loss;
• 正则化相当于在我们优化的过程中添加了限定条件, 如
  • 等值限定条件:
    • $$\begin{align*}&min \quad f(x)\\ & s.t. \quad h(x) = 0\end{align*}$$
    • 
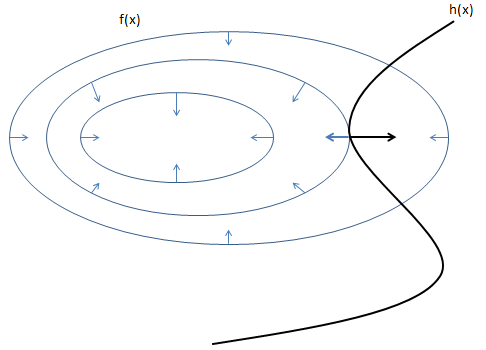
    • 如果不添加该限定条件, 那么应当按照f(x)的极值点来求, 也即是找到$\frac{\partial{f(x)}}{\partial{x}} = 0$的点;
    • 但是由于$h(x)=0$这一条件的存在, 我们只能选择在上图黑线上的点, 由等值线可知, 越往圈内越小, 故最小值在图中相切处取得;
      • 也只能在相切处取得, 因为若是相交, 则说明:
        • 往圈内走还有别的取值线与之相交, 也即是说:
        • 沿着圈向内还能取到更小值;
    • 所以也就是说, 对于f(x)和h(x)而言, 在相切的地方, 两个函数的梯度一定在同一条直线上, 可以表示为:
      • $$\nabla f(x) = \lambda \times \nabla h(x)...(1)$$
    • 变化一下式子:
      • $$\nabla f(x) +\lambda \times \nabla h(x) = 0...(2)$$
    • 这就又回到了起点, 我们再对$\lambda,x,y$分别求偏导, 并使偏导等于0, 再解方程组即可;
    • 那么对于多个约束的情况呢?
      • 上面我们得到了:
        • $$G(x) = \nabla f(x) +\lambda \times \nabla h(x) = 0...(3)$$
      • 再加一个约束$h_2(x)=0$, 也无非是:
        • $$\nabla G(x) +\lambda_2 \times \nabla h(x) = 0...(4)$$
      • 再多来点也无非是:
        • $$L(x,\lambda)=f(x)+\sum_{i-1}^{n}\lambda_{i}\nabla h_{i}(x)...(5)$$
      • 然后对$\lambda_i,x$求偏导, 使其等于0;
    • 对于等式约束和不等式约束混合:
      • 
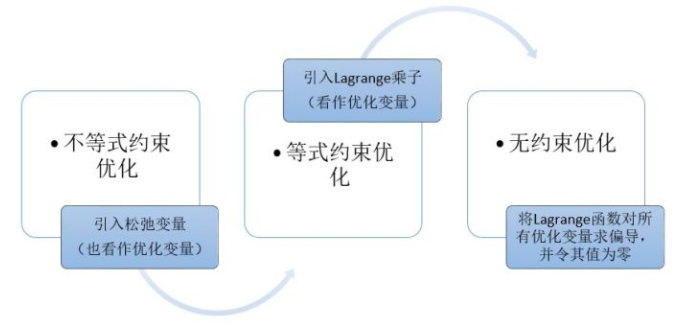
      • 又要分为两个情况:
        • 由于一个在可行域内部的h(x)上的点, 如果他不是f(x)的极值点[下图左], 那么除非h(x)在该点处与等值线相切,并且位于边界处,就能够沿着h(x)在可行域内找到f(x)更小的点;
          • 
        • 因此实质上只有两种情况:
          • 上图右:在 h(x) 和 等值线相切的地方[并且是边界处]
            • $$\nabla f(x)+\lambda \nabla h(x)+\mu \nabla g(x) = 0\\ h(x)=0\\ g(x)=0\\ \mu \geq 0...(6)$$
            • 由图可知, 越往外值越大, 故而g(x)的梯度方向是向外的, 而f(x)的极小值点在中间, 也即其梯度是向内的;
            • 所以二者梯度相反, 所以对应(1)式中$\lambda<0$, 变化为(2)的形式后自然大于0了;
          • 上图左:f(x) 的极值点本身就在可行域里面。
            • 等于没有不等式约束;
      • 用松弛变量的方法引入:
        • 将$g(w_i)<0$变为 $h(w_i) = g(w_i)+a_i^2 =0$, 再作为无约束优化求解:
        • 
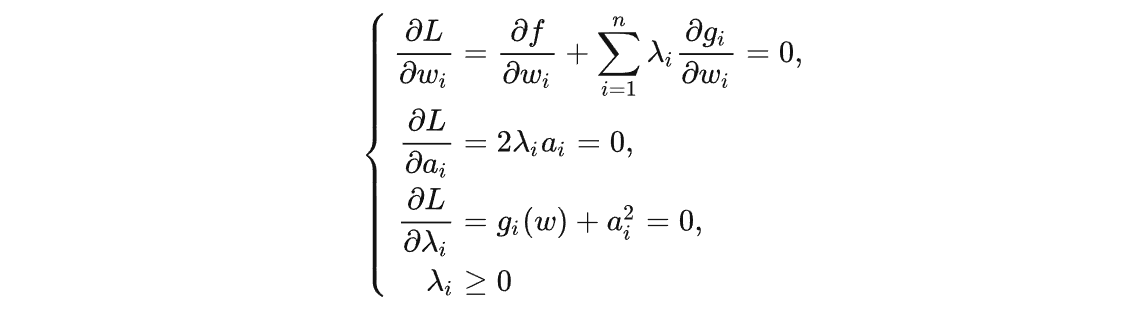
        • λ为什么大于0?
          • 同上面集合方法的证明;
        • 对于$\lambda\times a_i = 0$,有两种情形(对应上面)
          • 情形1:$\lambda_i=0,a_i\neq 0$
            • $\lambda_i=0$, 相当于没有约束
          • 情形2:$\lambda_i\neq0,a_i=0$
            • 此时$g_i(w) = 0$,且$\lambda_i>0$;
      • 如何在一个方程里面显示出来:[也就是KKT条件]
        • $$\nabla f(x)+\lambda \nabla h(x)+\mu \nabla g(x) = 0\\ \mu g(x) = 0\\ \mu \geq 0 \\ h(x)=0\\ g(x) \leq 0...()$$
        • 这个优化问题的极值点一定满足这组方程组。
        • 不是极值点也可能会满足，但是不会存在某个极值点不满足的情况;
        • 也即该优化问题取得极值的必要条件;
• 回到L1,L2正则化, 我们可以用只有两个权值w1,w2的模型作为例子;
  • 
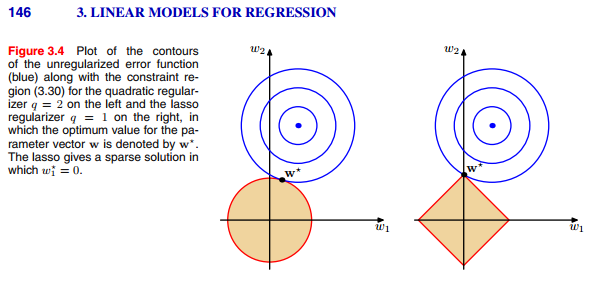
  • 对于L1正则化(右图):
    • 它将原本在整个坐标系的解空间, 限制到了方形的边缘上(不等式限制$w_1+w_2\le C$)
    • 而等值线与菱形端点相交的概率要大很多, 所以会有权值在最优时取到0(端点位于坐标轴上),至于为什么概率会更大:
      • 在不加约束的条件下, loss函数中心的位置落于红色区域,则等值线与端点相交[取一个点,灵活半径画圆,总是最先碰到端点];
        • 
      • 将图线不断延伸, 即可发现红色区域面积远大于白色区域[或许截个圆比较合适]
  • 对于L2正则化(左图), 圆形区域对于任意极值点, 边缘上每个点被取到的概率都一样;

    设输入向量x=[1, 1, 1, 1]，两个权重向量$w_1=[1, 0, 0, 0]，w_2=[0.25, 0.25, 0.25, 0.25]$。那么$w_1^Tx=1,w_2^Tx=1$，两个权重向量都得到同样的内积，但是w1的L2惩罚是1.0，而w2的L2惩罚是0.25.因此，根据L2惩罚来看，w2更好，因为它的正则化损失更小。从直观上来看，这是因为w2的权重值更小且更分散。所以L2正则化倾向于是特征分散，更小。

损失函数:

• 类型:
  • 0-1损失:
  • 平方损失:
  • 绝对损失:
  • 对数损失:
• 直接将(f(x),y)带进Loss函数去算,得到的是单个预测的损失;
• 我们要验证决策函数f的优良性, 应当求其期望:
  • 输入输出遵循联合分布P(X,Y),则期望损失:
    • $$R_{exp}(f) = E_P[L(Y,f(X))] = \inf_{\kappa\times y}L(x,f(x))P(x,y)dxdy$$
  • 然而我们无法知道P(X,Y) [这正是我们需要的], 故而我们只能用已知的—训练集的损失, 也即经验损失:
    • $$R_{emp}(f) =\frac{1}{N}\sum_{i=1}{N}L(y_i,f(x_i)$$
  • 根据经验风险最小化求最优:
    • $$\min_f \in F{\frac{1}{N}\sum_{i=1}^N{L(y_i,f(x_i))}}$$
  • 就如同下图, 忽略黑线, 能够直接取到最中心的等值线[最小值];
    • 
  • 然而我们在这种情况下求到的只能是过拟合的, 因为根据大数定律, 只有当样本量无穷大的时候,我们才能让经验风险接近期望风险;
  • 我们当然不希望过拟合(这意味着我们得到的模型只是贴近于训练数据集),因此我们要为其加上正则项:
    • $$R_{srm}(f) =\frac{1}{N}\sum_{i=1}{N}L(y_i,f(x_i)+\lambda J(f)\\ srm = structural risk minimization\\ J(f) = 模型复杂度$$
    • 关于正则化可查看什么是正则化
    • 这时,当结构风险过小,也即模型过于复杂时[含有多个非零参数],第二项模型复杂度会比较大,因而不会被选取;
• 泛化误差: 刚才我们讲到的是对于训练数据集的风险, 最小化其得到模型f,用这个模型去预测没被用来训练的数据, 就可以得到泛化误差:
  • $$R_{exp}(\hat{f}(X)) = E_P[L(Y,\hat{f}(X)] = \inf_{\kappa\times y}L(x\hat{f}(X))P(x,y)dxdy$$
  • 泛化误差也叫out of sample error,因为是经过最小化风险得到的模型, 参数已然确立, 相当于测定模型离真实值的偏离程度;